

For centuries people pondered lightning, lodestones, static electricity and other electromagnetic phenomenon without developing even rudimentary explanations or models. (I am summarily dismissing "Zeus throwing bolts" as an explanation!) It is hard to imagine anything as dramatic as lightning going completely unexplained in our modern technical world but, to be fair, electricity is usually invisible and, without electronic gadgets, it is rather elusive. Fortunately, today’s electronics experimenter has no shortage of electronic gadgets and electricity is available "on tap" at the nearest electrical outlet! Even a poorly financed experimenter can acquire precision equipment that would have served proudly in a modern laboratory only a few decades ago and junk yards have mountains of scrap electronic components that would have been worth a fortune to that same lab. The concepts are simple and materials are at hand, so it is time to begin the adventure into electronics.
Electrical interactions are surprisingly simple and a few basic laws of electricity model the real world with stunning precision. Quantum physics has shown that the theories of Faraday, Maxwell, and other scientists of the nineteenth century were "only" excellent approximations of a much more bizarre set of phenomena but the fundamental mathematical relationships they discovered are the workhorses of modern technology; virtually all modern technological advancement flows from the extreme predictability of electricity and magnetism.
Lets start our discussion with a quantum concept: As far as anyone knows there is a minimum quantity of charge - an amount of charge that cannot be subdivided under normal circumstances. This is the amount of charge that an electron and proton possess. (The Standard Model of physics says the proton's charge is actually made from three quarks, two of which contributes 2/3 of the charge and another that contributes -1/3 of the charge for a sum of 1. Whether quarks "really" have these fractional charges is debatable. These quarks cannot be seen directly and it takes high energy atom "smashers" to see evidence of their individual existence and the individual charges. Quarks "must" combine in such a way to create integer values of charge when forming matter and may be considered to be "virtual" particles that don't "exist" by themselves. This is curious stuff but lets just say that you won't run into fractionally charged particles at your workbench!) This packet of charge has a magnitude denoted by e and comes in two "polarities" denoted by the plus and minus signs (positive and negative). All electrical charges are made up of these tiny packets and charges with the same polarity physically repel each other and opposite charges attract each other. The electron charge is defined as the negative charge, thanks to Benjamin Franklin. (It might be nice if the electron were considered positive but changing now would make changing from English to Metric look like a cake walk!) A little more that 6,240,000,000,000,000,000 electrons are needed to make the common unit of charge called the coulomb. The unit of current, the ampere, is defined as the flow of one coulomb per second. Clearly, the charge on one electron is rather small. If the electric charge on the electron were represented by a drop of water, one coulomb would fill a lake more than 30 miles across and over 100 feet deep. The current flowing in a one amp flashlight bulb is one such lake per second! Despite this incredible flow rate, an electron entering a wire at the battery might take the good part of a minute to reach the bulb. Obviously, there are an inconceivable number of free electrons in the wire! As you might surmise, most electronic circuits deal with astronomical numbers of electrons and the discrete nature of the charge carriers is insignificant.
Since there are 6.24 x 1018 electrons in a coulomb, the charge on a single electron is 1/(6.24 x 1018 ) coulombs or 1.6 x 10-19 coulombs.
R.A. Millikan and associates are credited with being the first to accurately measure this charge using an ingenious apparatus in what is now known as the Millikan oil-drop experiment:
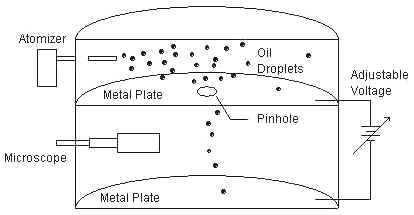
Tiny drops of oil from an atomizer were injected between two metal plates with an adjustable voltage between them. The resulting electric field would attract one polarity of charge to the top plate and if the voltage was just right, the force of gravity could be perfectly balanced, freezing the particle in mid-air. At this point, gravity times the drop’s mass equals the charge times the electric field. Millikan discovered that the random charge on the droplets was always an integer multiple of 1.6 x 10 -19 coulombs. The methods used to calibrate the apparatus are detailed in many physics texts and are well worth reading! Pay special attention to the technique used to determine the drop’s mass and ponder whether you would have had confidence in the measurement!
Lab Assignment:
You should have observed the expected attraction of the neutral particles to the charged plastic but the careful observer will also notice that many of the attracted particles will suddenly fly away from the rod after a minute or two - as if repelled. The reaction is nearly immediate if the little pieces of paper are slightly damp. Try dropping a damp piece of paper or a tiny piece of aluminum foil past the charged plastic. It will be attracted, but as soon as it touches it will fly away. The rapid, erratic motion is hard to follow so watch carefully!
The charge on the rod attracts the "neutral" particle but as soon as contact is made the particle picks up some of the charge and the like charges repel each other. Dry particles do not pick up the charge as quickly because they are less conductive and remain attracted to the rod for a longer period.
| If you have never done these experiments then it is important that you do them now. No amount of study replaces real-world experiences. Millikan’s amazing experiment was the result of sound scientific reasoning combined with an engineering common-sense that comes only from tinkering. You have charged rubber balloons to stick them to the wall, no doubt! But did you ever determine if the charge on the balloon is the same polarity as the change on your pocket comb? How about a glass rod rubbed with silk? See if you can find out through experimentation. Hint: Like charges repel - opposites attract. Another Hint: Glass and silk are positively attractive whereas cheap plastic and fake fur have negative connotations! (Puns intended!) |
You might be wondering why I added quotes to "neutral". Well, the force between two tiny particles with charges q1 and q2 is given by Coulomb’s Law:
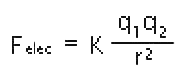
where K is the "dielectric constant" near 9 x109 and r is the distance between the charges. This force is a vector that points along the line between the two charges. But wait! Something is wrong! If the force is proportional to the product of two charges then why does the charged plastic rod pick up neutral particles? Since one of the charge terms is zero shouldn’t the force be zero? The answer is not obvious and may leave one wondering if the equation has any "real world" relevance. When the charged rod is held near a small object, a charge is induced in the object. If the object is a conductor, the like charges will be repelled to the far side of the object and the opposite charges will be attracted to the side nearest the charged rod. Since the charges are segregated at different distances, their contribution to the total force will be different (note the 1/r 2 term). The charge carriers in an insulating material are not free to move about as in a metal but the charge can redistribute on a microscopic level resulting in a somewhat weaker attraction to the charged rod. If a conductive object is touching a conductive surface, it can accumulate a net charge since like charges can leave the object entirely and opposite charges can accumulate and the resulting attraction can be quite strong. Try attracting little pieces of aluminum foil sitting on a metal cookie sheet. Make sure the foil pieces aren't laying flat by wrinkling or bending them a bit. They should fly off the metal sheet with enthusiasm!
Coulombís Law assumes infinitely small particles and induced charge cannot form since there is nowhere for the charge to go! We can illustrate the phenomenon with a simple experiment:
Lab Assignment:
This experiment will require the construction of a unique differential electroscope. The traditional electroscope consists of two metal leaves hanging freely from a wire like a sheet draped over a clothes line. The leaves are usually placed inside a glass jar to block the wind. The wire protrudes through an insulated top to allow for the deposition of charge. But this unique differential electroscope has two isolated supports for the metal leaves (one leaf per support) allowing a different charge to be applied to each leaf. For the purposes of this experiment, construction can be quite simple requiring only a small block of Styrofoam, two large nails and a couple of strips of aluminum foil about 4 inches long and 1/2 inch wide. Push the two nails through the foam about 1 1/2 inches apart forming two hangers for the foil strips. Bend the ends of the foil strips around the nails so that the strips hang freely, easily swinging back and forth. Make sure they are hanging straight down, unlike the photo where they are slightly attracted to each other. The foam can hold a charge and it isn't always easy to tell if the leaves are charged or just bent. If you have trouble, try connecting an earth ground to both nails before adjusting the leaves to make sure there is no charge. They need to be parallel or induced charge will occur across the length.

Collect some charge on your plastic rod or pocket comb and transfer the charge to one of the leaves by dragging the charged rod across the head of the nail on the back side of the foam. (Do not touch the other nail!) Notice that only a little attraction or perhaps a slight repulsion is noted between the strips. Now touch the head of the nail supporting the uncharged strip. The two strips slam together!
Because the strips are very thin compared to the distance between them the amount of force due to the induced charge is small. Whether the charge is on one face of the leaf or the other it is almost the same distance from the other leaf so 1/r 2 is about the same. Since the net charge on the neutral leaf is zero, the force between the leaves is nearly zero. But when you touch the neutral leaf, the induced charge can skyrocket since there is now a place for the like charge to go and a plentiful source of opposite charge (your body).
A comb picking up little particles involves induced charge - not simply different levels of charge. Attraction occurs because the charged rod induces a significant opposite charge or polarization in the otherwise neutral objects. It is an important distinction - one would be wasting time trying to attract neutrons with an electric field even though a charged rod seems to attracts "neutral" particles!
A coulomb is one amp for one second, a modest sounding amount of charge but actually a coulomb is an extremely large electrostatic charge. According to Coulomb’s Law, two plates one yard apart each with one coulomb of charge will attract or repel each other with billions of pounds of force! Obviously, charged bodies usually contain much less than a coulomb!
By the way, most of the world and all of science uses one of two metric-based systems for calculations, the mks and the cgs systems. Mks stands for meters, kilograms, seconds and cgs stands for centimeters, grams and seconds. For those of us more familiar with the system of feet, pounds and seconds the metric system is becoming more and more necessary. But a troublesome unit is the newton which is the unit of force in the mks system. One newton is 0.225 pounds. The kilogram is a unit of mass and on the earth a kilogram will weigh (experience a force of) 2.21 pounds due to gravity. Kilograms are commonly used as a weight instead of a mass since most of us spend our entire lives in the earth’s gravitational field. But pounds (weight) and kilograms (mass) are not really interchangeable. A person will still have his kilograms in the weightlessness of space but his bathroom scale will indicate zero pounds of force. Weight scales that indicate kilograms only function properly in the earth’s gravity - they assume earth’s gravity when determining the kilogram mass. This careless mixing of weight and mass units can make scientific calculations a bit confusing at times! As a memory aid, imagine Isaac Newton sitting under the apple tree pondering his famous equation, F = MA. The force, F, is appropriately in "newtons"! (Cover your ears when you hear an engineer discussing grams of force.) The acceleration of gravity is 9.81 m/sec2 so the number of newtons is 9.81 times greater than the number of "kilograms of force". That is pretty close to 10 so if a weapons engineer tells you that it takes 2 kilograms of force to detonate his new mine you can estimate the required force to be 20 newtons. The dielectric constant of space in the mks system is 9 x 109 nm2 /coul2 .
Therefore, in the above example of two, one coulomb charges separated by one meter, Coulomb’s Law predicts 9 x 109 newtons (a couple of billion pounds.):
![]()
The Electric Field
The acceleration term in Newton’s equation, F = MA, is also the gravitational field intensity when calculating the effects of gravity on masses. In fact, Einstein argued that acceleration and gravity were indistinguishable! The concept of a gravitational field is familiar to most people so the concept of an electric field is readily described. We can define an electric field as we would define a gravitational field - the gravitational field strength is the ratio of an objects weight to its mass. The electric field is defined as the ratio of the force to the charge causing the force. The equivalent equation to F = MA is F = qE where E is the electric field intensity. Electric fields act just like gravitational fields with one interesting exception! The force on a charge due to an electric field can have two polarities but gravity only attracts (so far as we know).
Here is an exercise:
Suppose that the distance between an electron and the proton in a hydrogen atom is 5 x 10-11 meters. What is the force attracting the electron? This is an easy problem! (Although you might have to look back a few paragraphs.) You know the charges of the particles (the smallest charge that exists, 1.6 x 10-19), the distance and the dielectric constant of the space in between (9 x109). See if you can calculate about 9 x 10-8 newtons.
Hobby Project: Building Classic Electroscopes
 |
Although the electroscope is a bit obsolete, they still possess a charm and elegant simplicity. The classic electroscope is constructed in a large clear glass jar or bottle with an attractive brass wire hanger for the foil leaves and a polished brass knob at the top for the electrode. Laboratory grade electroscopes used extremely thin gold foil to minimize the weight and therefore maximize the deflection. Similar voltage sensitivities may be achieved with aluminum foil if very long leaves are used. The "capacity" will be higher so more charge will be necessary but the sensitivity to voltage can be quite good. Here is a picture of an electroscope built into a large, clear wine bottle with 11 inch leaves. They are simply fastened to a bolt which protrudes through the cork. This electroscope will visibly respond to potentials under 100 volts! It is desirable to choose a wider jar than this wine bottle so that the leaves do not become attracted to the glass sides when highly charged. Various chemistry beakers make attractive electroscopes with necks suitable for stoppers and wide chambers for the leaves. Hanging short leaves can be a bit tricky since they must swing independently. Give one leaf arms for hanging like a person hanging from a bar. The other leaf has a single narrow arm in the middle like a monkey hanging by its tail! The two leaves can move away from each other without the pivot points interfering with each other. The long leaves in the picture were simply attached to the screw on the top since they are long enough to flex. Smooth the leaves by gently rubbing them with a finger against a flat surface. |
If you wish to make an electroscope with a scale, replace one of the leaves with a stiff strip of metal or copper-clad circuit board. Fasten the flexible leaf to the stiff leaf at the top and place a paper scale behind the leaves. If the flexible leaf is at least 1/2" wide it will be stiff enough to not twist and stick to the scale. Enclose the scope in a large, clear plastic box with square sides - the type sold for decorative purposes will do nicely. A colored Lucite rod mounted in a wooden handle makes a nice accessory for this unique conversation piece. Actually, ordinary glass bottles are inferior to clear plastic bottles due to surface conductivity. So, if you want the very best performance, consider using a clear plastic jug, jar or box. Hobby Project: Building a Leyden Jar |
|
| After experimenting with comb and an electroscope for a few minutes, the experimenter will notice that the electroscope leaves can be charged in steps - each touch of the comb causes more deflection. The leaves accumulate the bits of charge and the voltage builds. Bigger leaves will require more charge to achieve the same voltage because the electrons are spread over a larger area. If we coat the entire insides of the jar with aluminum, the capacity of the jar to hold charge will be much higher - and it will have a name! Named for its discovery by the physicist Pieter van Musschenbroek at the University of Leyden in the mid 1700s, the Leyden Jar is a simple form of capacitor that belongs in every electrostatics laboratory. | |
| The first Leyden Jar was simply a water-filled jar with a wire electrode dipped into the water (tap water is a conductor). A more modern version is made by lining the inside and coating the outside of the jar with aluminum foil forming two capacitor plates. The attraction of opposite charges between the two plates gives the foil Leyden Jar the capacity to store a significant charge. The outer foil is usually the "ground" plate and the inner foil is the "hot" plate. A connection is made to an electrode on the top of the jar and the foil with a wire or metal chain. The Leyden Jar in the photo was made from an empty spaghetti sauce jar, a rubber stopper, a long screw, aluminum foil, and black electrical tape. Spray adhesive was used to affix the foil to the inside surface and the electrode connection was made by tangling a long piece of bare wire with some of the foil on the inside and fastening the other end to the screw with electrical tape. A ground wire was fastened to the outer foil and the foil was wrapped with a coating of fiber tape for protection. A one inch gap was left at the top of the jar for insulation. This gap should be cleaned with alcohol and wrapped with electrical tape to enhance the insulation. A plastic jar will hold a charge better, by the way, and no tape is necessary. |  |
| The jar may be tested by connecting it to an electroscope with a stiff wire that touches only the electrodes. A few discharges from a charged pocket comb or plastic rod should give an indication on the electroscope. If the electroscope discharges quickly, there is too much leakage -probably due to dirty glass or too much humidity in the air. Electrostatics experiments are best performed on dry days! As with the electroscope, you will have an easier time with a clear plastic jar or box (try a peanut butter jar). If everything is working well, charge the Leyden jar with repeated comb charges then bring your finger near the electrode while holding the ground wire in the other hand. You should get a spark and the electroscope will indicate a sudden drop in charge. | |
Electric Fields
The concept of a "force field" is quite familiar to us earth-bound humans. We spend our entire lives in the earth’s gravitational field which seems perfectly uniform and constant. The lines of force are clearly "down" - the direction the fine china heads when it slips out of our hands. A line of force is simply an imaginary line that traces the path an object would take due to the influence of a field. For diagramming purposes, it is useful to associate a line with a certain amount of force so that more lines indicate more force. A person standing on the moon would be "skewered" by fewer lines of force than a person standing on the earth since the moon’s gravitational field is weaker than earth’s. The force on an object is proportional to the line density - when the lines are far apart, the force is weak and when they are closely spaced, the force is high. Remember that the line density can be hard to judge since only a few lines are usually drawn; these lines are just a schematic representation of a continuous field. Lines of force are most useful for showing the general shape of a field - only hinting at the field strength at any particular point. One could draw so many lines that they blur together giving shades of gray, darkening in areas of greater force, but it would be difficult to determine the direction of the force if the individual lines could not be seen. The following figure shows typical lines of force for an attracting body and a simulation of how the lines of force might look if thousands were drawn. Remember, as an object moves along a line of force it usually encounters a changing level of force.
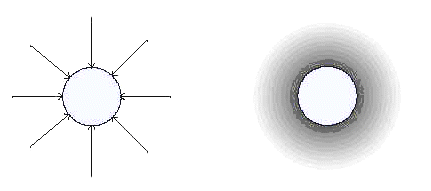
The lines of electric force are defined to point in the direction a positive charge would move so electrons have lines of force pointing at them and protons have similar lines of force pointing away. When several charges are in close proximity, the line of force at a particular point will be the vector sum of the contributions from all of the charges:
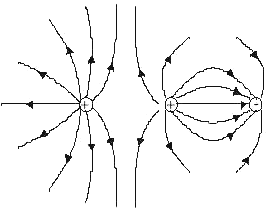
Unlike the gravitational field we know, electric fields have two polarities and can work together or oppose each other as the diagram shows. Notice how a positive particle precisely between the two positive charges would experience no force since the two fields cancel. But if the charge is slightly above or below the center line, it is squeezed out like a watermelon seed between wet fingers! Just like gravity, the electric field is a "force field" - the field intensity at any point is equal to the amount of mechanical force that would be applied to a charge of one coulomb positioned at the point. The units are newtons per coulomb. The electric field surrounding a charged Lucite rod can be detected by holding the rod near the electrode of a sensitive electroscope. Without the rod making contact, the leaves will spread due to the induced charge caused by the field.
Voltage
When you climb on the roof of your house the earth’s gravity has the potential to do you great harm. In fact, your body has potential energy which is proportional to your height off the ground. If you slip, you will accelerate and accumulate kinetic energy until something stops you (hopefully, a soft pile of hay). The scientific term, work, is defined as force multiplied by distance. So gravity does work on you as you fall - the force is your weight (mass times gravity) and the distance is the height of the roof. The total amount of work done on you during your fall determines how hard you hit! Since gravity is uniform, you can gauge your safety by peeking over the edge of the roof to see how high you are. But if gravity were not uniform, you would need to multiply the height by the local gravity to determine how much potential energy your body has (which is equal to the kinetic energy it will have when it hits the ground).
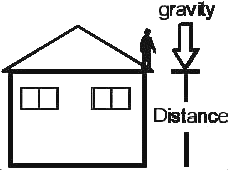
When dealing with charges and electric fields, this product (meters times newtons per coulomb) is referred to as "voltage". In a uniform electric field, the voltage between two points is the product of the magnitude of the electric field and the distance between the points. A charged particle will "fall" or accelerate in the electric field just as a body will accelerate in a gravitational field. The farther it falls, the more kinetic energy it accumulates. So the voltage between two points tells us how much energy will be imparted to a unit charge moving between them. Multiply the voltage by the amount of charge to get the energy (in newton-meters which are called joules).
For example, a single electron with a charge of 1.6 x 10-19 coulombs will pick up 1.6 x 10-16 joules moving between two points with 1000 volts of potential difference:
1.6 x 10-19 coul x 1000 volts = 1.6 x 10-16 joules
Notice that we did not need to know the physical dimensions or the magnitude of the electric field -these quantities are already combined in the "voltage". It is a handy combination since much of electronics involves the effects of potential differences regardless of the distances involved or the resulting electric fields. In your car, wiring carries the battery’s 12 volt potential difference to various motors, lamps and assorted gadgets in different locations and the electric field within the car is a complex three-dimensional structure. But the concept of voltage lets us greatly simplify the description of the functioning of the auto’s wiring without regard to the path the charges follow.
| The electron that moved across the potential difference of 1000 volts in the above example gained 1000 "electron-volts" - a unit of energy commonly used in particle physics. One electron-volt is the amount of energy a single electron picks up when it accelerates through one volt. The electron-volt is a measure of energy - not voltage. Electron-volts and joules are the same type of quantity. (1 ev = 1.6 x 10-19 joules) |
You may have already noticed that the "units" of voltage are joules/coulomb which is an amount of energy (work) per unit charge. You could say, "my vehicle’s voltaic pile performs 12 joules of work moving one coulomb of charge from one terminal to the other." (Or you could say, "my car has a 12 volt battery.")
Now here is where it gets a little tricky! You have probably heard voltage referred to as "electromotive force" or emf and you have probably heard knowledgeable folk say that voltage is "how hard the electricity is pushing". But from the previous discussion it would seem that the electric field is the force and that voltage is the amount of work done on (or energy imparted to) a charge moving in the electric field. So what is all this talk of emfs? Well, its a bit of a word shortcut. A higher voltage battery will generate higher electric fields in a given circuit and that is why more work will be done on the charges moving in the circuit. Remember how the concept of voltage let us sidestep the difficulties of knowing the electric field distribution and the physical movement of the charges. We know that electric fields are doing the "pushing" and the charges are moving some distance but what really matters is how much real work is being done.
Its a bit like saying someone hit the baseball with a lot of "force" instead of "energy". Actually, the bat does deliver some number of joules per baseball depending upon the speed of the swing so a batter’s "voltage" could be defined! And it would be natural to refer to this "work per baseball" as a "force" even though it isn’t newtons.
Here is a silly analogy. Suppose one postal employee can toss one pound packages 15 feet and another can toss them 30 feet. The second employee could be said to have a higher "voltage" since he is doing more work per unit weight. We could say he has a parcel-motive force of 30. Actually, the force he applies to the package is not 30 and calling the work he did on the package a "force" is not entirely correct but the meaning is clear enough - he "motivates" the parcel 30 feet.
Lab Assignment:

Here is an interesting voltage experiment which will literally cost you a pile of money! Count Alessandro Volta’s voltaic pile was the first and probably the simplest battery ever made. To duplicate this important invention you will need 10 pennies, some aluminum foil, some cardboard (try the back from a pad of paper), some saltwater and a voltmeter to measure the results. Cut a one inch square of aluminum foil for the base of the pile. Place a penny in the center of the aluminum. Now cut 9 disks of cardboard and foil the same size as a penny. The foil disks may be all cut at one time by folding the aluminum foil until 10 layer are stacked. (Squeeze the foil and a penny between a finger and thumb so that the penny may be used as a cutting guide.) Soak the cardboard disks in the saltwater for several minutes then place one of these paper disks on top of the first penny. Now place a small disk of aluminum foil on top of the wet paper. Keep building the stack repeating the pattern: foil, penny, paper, foil, penny, paper, etc. (Note that the pennies go directly on the foil - no paper.) When you run out of money, stop with a penny on top. Touch one probe of your voltmeter to the foil square at the base and touch the other to the penny on top. If you made the pile carefully, you should measure about 4 volts. The penny will be the negative terminal. Try touching an LED across this "battery" in a dimly lit room.
The concept of resistance can be readily demonstrated using this voltaic pile. Measure the voltage across the pile when the LED is connected and feebly glowing. Notice that the voltage is much lower than the voltage with only the voltmeter connected. Every electrical source has internal resistance - this pile has a pile of resistance! (Pun intended!) The resistance of the pile limits the current that can flow in the LED.
The mathematical relationship between voltage, current, and resistance is known as Ohm’s law:
V = I x R
"V equals I times R" may be manipulated to give equally simple equations for resistance and current:
I = V / R and R = V / I

This Ohm’s Law Circle is an easy way to remember the three formulas. The voltage, V is I times R since they are next to each other. R is "V over I" and I is "V over R".
Ohm’s Law is intuitive: One would expect more current to flow in a resistor if the voltage across it is increased and one would expect less current to flow if the resistance is increased for a given voltage. The penny battery has an electromotive force of about 4 volts and it will supply about 1 milliampere. Try switching your voltmeter to the current scale to see for yourself. How much internal resistance does the pile have? You could model your penny battery as a "perfect" 4 volt source in series with this resistance. (Such a model is called the "Thevenin Equivalent".) Modern batteries have much lower internal resistance and can supply far more current due to their superior "chemistry" and physical design.
You now have the tools to begin your study of basic circuits.
In day-to-day electronics work, voltage is simply thought of as an "electromotive force" without much attention paid to the units of "joule per coulomb". The units of current are sometimes contemplated when calculating the coulomb charge on a capacitor but it is more common to refer to the energy stored in the capacitor or the voltage rather than the coulombs. (In electrochemistry the coulomb has a high visibility since the products of electrolysis are directly proportional to the total charge that flows.) The fundamental units of the ohm are rarely mentioned in polite company (joule-second per coulomb2 ). In fact, the electric field strength is usually referred to in units of "volts per meter" instead of "newtons per coulomb" because voltage is readily measured whereas the force on a charge is rather difficult to measure. So, in most instances, "volts", "amps", and "ohms" are among the units of choice when discussing electronic circuitry.
Philosophical Point: You should work through the fundamental units several times until you achieve the emotion of full understanding - at which point you may forget them without suffering the debilitating effects of the emotion of not understanding. You can always look them up to "refresh" your memory. Ask a few electronics engineers to tell you the fundamental units of volts or ohms. Be polite. Just say, "Oh, I see".