

When I first read of Bell's Inequality, it seemed rather odd. I tried to draw a Venn Diagram to see if it made sense graphically. The following graph resulted and, although not strictly a Venn diagram (more of a pie chart, really), it seems to prove the theorem and give the value of the inequality to boot.
Bell's Inequality (in a simple, comprehensible form anyway) states that in a group of items that possess three properties, A, B, and C, the number of items that possess property A but not B plus the number of items that possess the property B but not C is greater or equal to the number of items that possess property A but not C. For example, lets say that my transistor bin has some Silicon and Germanium transistors (property A = "silicon"), some of each have gain over 100 and some under 100 (property B = "gain over 100"), and some are NPN and the others are PNP (property C = "PNP"). Bell's Inequality states that the number of silicon transistors with gain up to 100 plus the number of NPN transistors with gain over 100 is greater than or equal to the number of silicon NPN transistors. That's seems a bit surprising at first but the graph below clearly shows this result. To keep the clutter down, "the number of items with property..." was left off the equations and chart. So "A, Not B" means the number of items with property A but not possessing property B.
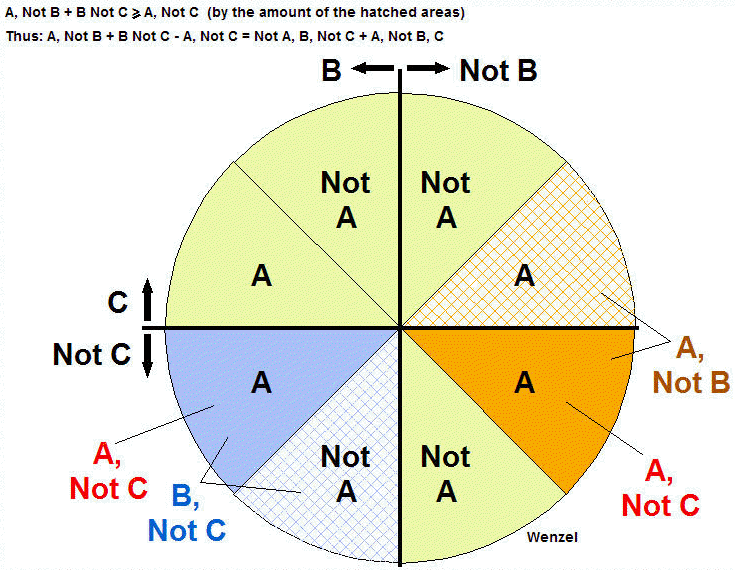
The circle (pie tin) is divided into 8 "bins" with the left bins containing items with property B (gain over 100), the upper bins containing items with the property C (PNP). (Low gain transistors are on the right and NPNs are below.) Property A (silicon) has two bins in each quadrant to accommodate all possibilities. All items now have a home on this chart.
The first term in Bell's Inequality denotes items with property A but not B denoted by orange and the second term denotes items with property B but not C denoted by blue.
It is immediately obvious that items with property A but not C (solid blue and solid orange) are included in the first two categories denoted by both hatched and solid blue and orange bins.
A, Not C is clearly a subset of B, Not C + A, Not B with the excess, if any, in the hatched bins.
Well, that seems obvious. The hatched bins would need to contain "negative" transistors for the sum of the blue and orange bins (solid and hatched) to be less than just the solid bins alone. No antimatter transistors, please! This graph actually lets us "solve" the inequality in that the amount of the inequality is simply however many items are in the hatched bins, Not A, B, Not C plus A, Not B, C. In the transistor example that would be the number of germanium transistors with a gain over 100 plus the number of silicon PNPs, plus the number of NPNs with gain below 100. Here's how the "solved" inequality sounds:
The number of silicon transistors with gain less than or equal to 100 plus the number of PNP transistors with gain over 100 minus the number of silicon NPN transistors is equal to the number of NPN germanium transistors with a gain over 100 plus the number of low gain silicon PNPs! It isn't so obvious in words, is it?
Here is an example parts selection:
| Type | Gain | Pol. |
| Silicon | High | NPN |
| Silicon | High | NPN |
| Silicon | High | NPN |
| Silicon | Low | PNP |
| Silicon | Low | PNP |
| Silicon | Low | PNP |
| Ger. | High | NPN |
| Ger. | Low | PNP |
| Ger. | Low | PNP |
| Ger. | Low | PNP |
Lets see if it works:
Property A = silicon
Property B = high gain
Property C = PNP
A, not B = Silicon, Low Gain (two orange bins) = 3
B, not C = High Gain, NPN (two blue bins)= 4
A, not C = Silicon, NPN (solid orange and blue bins)= 3
3+4 is greater than 3 (by 4) so Bell''s Inequality is true.
But does the "solution" work:
Not A, B, not C = germanium, high gain, NPN = 1
A, not B, C = silicon, low gain, PNP = 3
1+3 = 4 which is the amount of the inequality.
In quantum mechanical systems where particles are "entangled" the number of items in the solid orange and blue areas can seem to exceed the number of items in all four colored bins. That's just crazy talk. I've had that trouble with entangled transistor leads, too. The trick is to glue down the little plastic partitions so the transistors can't slip underneath. Glad I could clear that up.